跳转至

凸包

二维凸包

定义

凸多边形

凸多边形是指所有内角大小都在 \([0,\pi]\) 范围内的 简单多边形。

凸包

在平面上能包含所有给定点的最小凸多边形叫做凸包。

其定义为：对于给定集合 \(X\)，所有包含 \(X\) 的凸集的交集 \(S\) 被称为 \(X\) 的 凸包。

实际上可以理解为用一个橡皮筋包含住所有给定点的形态。

凸包用最小的周长围住了给定的所有点。如果一个凹多边形围住了所有的点，它的周长一定不是最小，如下图。根据三角不等式，凸多边形在周长上一定是最优的。

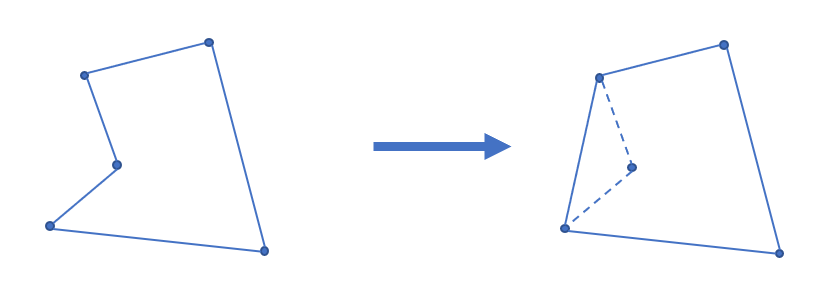
Andrew 算法求凸包

常用的求法有 Graham 扫描法和 Andrew 算法，这里主要介绍 Andrew 算法。

性质

该算法的时间复杂度为 \(O(n\log n)\)，其中 \(n\) 为待求凸包点集的大小，复杂度的瓶颈在于对所有点坐标的双关键字排序。

过程

首先把所有点以横坐标为第一关键字，纵坐标为第二关键字排序。

显然排序后最小的元素和最大的元素一定在凸包上。而且因为是凸多边形，我们如果从一个点出发逆时针走，轨迹总是「左拐」的，一旦出现右拐，就说明这一段不在凸包上。因此我们可以用一个单调栈来维护上下凸壳。

因为从左向右看，上下凸壳所旋转的方向不同，为了让单调栈起作用，我们首先 升序枚举 求出下凸壳，然后 降序 求出上凸壳。

求凸壳时，一旦发现即将进栈的点（\(P\)）和栈顶的两个点（\(S_1,S_2\)，其中 \(S_1\) 为栈顶）行进的方向向右旋转，即叉积小于 \(0\)：\(\overrightarrow{S_2S_1}\times \overrightarrow{S_1P}<0\)，则弹出栈顶，回到上一步，继续检测，直到 \(\overrightarrow{S_2S_1}\times \overrightarrow{S_1P}\ge 0\) 或者栈内仅剩一个元素为止。

通常情况下不需要保留位于凸包边上的点，因此上面一段中 \(\overrightarrow{S_2S_1}\times \overrightarrow{S_1P}<0\) 这个条件中的「\(<\)」可以视情况改为 \(\le\)，同时后面一个条件应改为 \(>\)。

实现

代码实现 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// stk[] 是整型，存的是下标
// p[] 存储向量或点
tp = 0;                       // 初始化栈
std::sort(p + 1, p + 1 + n);  // 对点进行排序
stk[++tp] = 1;
// 栈内添加第一个元素，且不更新 used，使得 1 在最后封闭凸包时也对单调栈更新
for (int i = 2; i <= n; ++i) {
  while (tp >= 2  // 下一行 * 操作符被重载为叉积
         && (p[stk[tp]] - p[stk[tp - 1]]) * (p[i] - p[stk[tp]]) <= 0)
    used[stk[tp--]] = 0;
  used[i] = 1;  // used 表示在凸壳上
  stk[++tp] = i;
}
int tmp = tp;  // tmp 表示下凸壳大小
for (int i = n - 1; i > 0; --i)
  if (!used[i]) {
    // ↓求上凸壳时不影响下凸壳
    while (tp > tmp && (p[stk[tp]] - p[stk[tp - 1]]) * (p[i] - p[stk[tp]]) <= 0)
      used[stk[tp--]] = 0;
    used[i] = 1;
    stk[++tp] = i;
  }
for (int i = 1; i <= tp; ++i)  // 复制到新数组中去
  h[i] = p[stk[i]];
int ans = tp - 1;

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
stk = []  # 是整型，存的是下标
p = []  # 存储向量或点
tp = 0  # 初始化栈
p.sort()  # 对点进行排序
tp = tp + 1
stk[tp] = 1
# 栈内添加第一个元素，且不更新 used，使得 1 在最后封闭凸包时也对单调栈更新
for i in range(2, n + 1):
    while tp >= 2 and (p[stk[tp]] - p[stk[tp - 1]]) * (p[i] - p[stk[tp]]) <= 0:
        # 下一行 * 操作符被重载为叉积
        used[stk[tp]] = 0
        tp = tp - 1
    used[i] = 1  # used 表示在凸壳上
    tp = tp + 1
    stk[tp] = i
tmp = tp  # tmp 表示下凸壳大小
for i in range(n - 1, 0, -1):
    if used[i] == False:
        #      ↓求上凸壳时不影响下凸壳
        while tp > tmp and (p[stk[tp]] - p[stk[tp - 1]]) * (p[i] - p[stk[tp]]) <= 0:
            used[stk[tp]] = 0
            tp = tp - 1
        used[i] = 1
        tp = tp + 1
        stk[tp] = i
for i in range(1, tp + 1):
    h[i] = p[stk[i]]
ans = tp - 1

根据上面的代码，最后凸包上有 \(\textit{ans}\) 个元素（额外存储了 \(1\) 号点，因此 \(h\) 数组中有 \(\textit{ans}+1\) 个元素），并且按逆时针方向排序。周长就是

\[ \sum_{i=1}^{\textit{ans}}\left|\overrightarrow{h_ih_{i+1}}\right| \]

Graham 扫描法

性质

与 Andrew 算法相同，Graham 扫描法的时间复杂度为 \(O(n\log n)\)，复杂度瓶颈也在于对所有点排序。

过程

首先找到所有点中，纵坐标最小的一个点 \(P\)。根据凸包的定义我们知道，这个点一定在凸包上。然后将所有的点以相对于点 P 的极角大小为关键字进行排序。

和 Andrew 算法类似地，我们考虑从点 \(P\) 出发，在凸包上逆时针走，那么我们经过的所有节点一定都是「左拐」的。形式化地说，对于凸包逆时针方向上任意连续经过的三个点 \(P_1, P_2, P_3\)，一定满足 \(\overrightarrow{P_1 P_2} \times \overrightarrow{P_2 P_3} \ge 0\)。

新建一个栈用于存储凸包的信息，先将 \(P\) 压入栈中，然后按照极角序依次尝试加入每一个点。如果进栈的点 \(P_0\) 和栈顶的两个点 \(P_1, P_2\)（其中 \(P_1\) 为栈顶）行进的方向「右拐」了，那么就弹出栈顶的 \(P_1\)，不断重复上述过程直至进栈的点与栈顶的两个点满足条件，或者栈中仅剩下一个元素，再将 \(P_0\) 压入栈中。

代码实现 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
struct Point {
  double x, y, ang;

  Point operator-(const Point& p) const { return {x - p.x, y - p.y, 0}; }
} p[MAXN];

double dis(Point p1, Point p2) {
  return sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));
}

bool cmp(Point p1, Point p2) {
  if (p1.ang == p2.ang) {
    return dis(p1, p[1]) < dis(p2, p[1]);
  }
  return p1.ang < p2.ang;
}

double cross(Point p1, Point p2) { return p1.x * p2.y - p1.y * p2.x; }

int main() {
  for (int i = 2; i <= n; ++i) {
    if (p[i].y < p[1].y || (p[i].y == p[1].y && p[i].x < p[1].x)) {
      std::swap(p[1], p[i]);
    }
  }
  for (int i = 2; i <= n; ++i) {
    p[i].ang = atan2(p[i].y - p[1].y, p[i].x - p[1].x);
  }
  std::sort(p + 2, p + n + 1, cmp);
  sta[++top] = 1;
  for (int i = 2; i <= n; ++i) {
    while (top >= 2 &&
           cross(p[sta[top]] - p[sta[top - 1]], p[i] - p[sta[top]]) < 0) {
      top--;
    }
    sta[++top] = i;
  }
  return 0;
}

闵可夫斯基和

定义

点集 \(P\) 和点集 \(Q\) 的闵可夫斯基和 \(P+Q\) 定义为 \(P+Q=\{a+b|a\in P,b\in Q\}\)，即把点集 \(Q\) 中的每个点看做一个向量，将点集 \(P\) 中每个点沿这些向量平移，最终得到的结果的集合就是点集 \(P+Q\)。此处仅讨论 凸包 的闵可夫斯基和。

例如：对于点集 \(P=\{(0,0),(-3,3),(2,1)\}\) 和 点集 \(Q=\{(0,0),(-1,3),(1,4),(2,2)\}\)，

将 \(P\) 沿 \(Q\) 的每个向量平移：

不难发现新图形也是一个 凸包：

性质

  1. 若点集合 \(P\)，\(Q\) 为凸集，则其闵可夫斯基和 \(P+Q\) 也是凸集。

    证明

    设 \(e,f\in P+Q\)，有 \(a,b \in P\)，\(c,d\in Q\) 且 \(e=a+c,f=b+d\)，则对任意 \(t\in[0,1]\) 均有：

    \[ \begin{aligned} te + (1-t)f &= t(a+c)+(1-t)(b+d)\\ &=(ta+(1-t)b)+(tc+(1-t)d)\\ &\in P+Q. \end{aligned} \]

    证毕。

  2. 若点集 \(P\)，\(Q\) 为凸集，则其闵可夫斯基和 \(P+Q\) 的边集是由凸集 \(P\)，\(Q\) 的边按极角排序后连接的结果。

    证明

    不妨假设凸集 \(P\) 中任意一条边的斜率与 \(Q\) 中任意一条边的斜率均不相同。将坐标系进行旋转，使得 \(P\) 上的一条边 \(XY\) 与 \(x\) 轴平行且在最下方。

    设此时 \(Q\) 中最低的点 \(U\)，\(P+Q\) 的 最低 且 靠左 的点 \(A\)。

    可知 \(\vec{A} = \vec{X} + \vec{U}\)，所以 \(A\) 必然在 \(P+Q\) 的边界上。

    同理，\(P+Q\) 中 最低 且 靠右 的点 \(B\) 有 \(\vec{B} = \vec{Y} + \vec{U}\)，也必然在 \(P+Q\) 的边界上。

    因此，有 \(\vec{AB} = \vec{XY} + \vec{U}\)。

    若按顺序进行旋转，则结果连续的构成了 \(P+Q\) 中的每条边。

    证毕。

实现

我们可以根据性质 2，将凸集 \(P,Q\) 极角排序，得到它们在 \(P+Q\) 上的出现顺序，把 \(P_1+Q_1\) 看做 \(P+Q\) 的起点，然后用类似 归并 的做法依次放边即可。

时间复杂度：\(O(n+m)\)

实现 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
template <class T>
struct Point {
  T x, y;

  Point(T x = 0, T y = 0) : x(x), y(y) {}

  friend Point operator+(const Point &a, const Point &b) {
    return {a.x + b.x, a.y + b.y};
  }

  friend Point operator-(const Point &a, const Point &b) {
    return {a.x - b.x, a.y - b.y};
  }

  // 点乘
  friend T operator*(const Point &a, const Point &b) {
    return a.x * b.x + a.y * b.y;
  }

  // 叉乘
  friend T operator^(const Point &a, const Point &b) {
    return a.x * b.y - a.y * b.x;
  }
};

template <class T>
vector<Point<T>> minkowski_sum(vector<Point<T>> a, vector<Point<T>> b) {
  vector<Point<T>> c{a[0] + b[0]};
  for (usz i = 0; i + 1 < a.size(); ++i) a[i] = a[i + 1] - a[i];
  for (usz i = 0; i + 1 < b.size(); ++i) b[i] = b[i + 1] - b[i];
  a.pop_back(), b.pop_back();
  c.resize(a.size() + b.size() + 1);
  merge(a.begin(), a.end(), b.begin(), b.end(), c.begin() + 1,
        [](const Point<i64> &a, const Point<i64> &b) { return (a ^ b) < 0; });
  for (usz i = 1; i < c.size(); ++i) c[i] = c[i] + c[i - 1];
  return c;
}

例题

例题 [JSOI2018] 战争

有两个凸包 \(P,Q\)，平移 \(q\) 次 \(Q\)，问每次移动后是否有交点。\(1\le n,m\le 10^5,1\le q\le 10^5\)。

实现 
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
#include <algorithm>
#include <cassert>
#include <cstdint>
#include <iostream>
#include <vector>
using namespace std;
using i64 = int64_t;
using isz = ptrdiff_t;
using usz = size_t;

template <class T>
struct Point {
  T x, y;

  Point(T x = 0, T y = 0) : x(x), y(y) {}

  friend Point operator+(const Point &a, const Point &b) {
    return {a.x + b.x, a.y + b.y};
  }

  friend Point operator-(const Point &a, const Point &b) {
    return {a.x - b.x, a.y - b.y};
  }

  // 点乘
  friend T operator*(const Point &a, const Point &b) {
    return a.x * b.x + a.y * b.y;
  }

  // 叉乘
  friend T operator^(const Point &a, const Point &b) {
    return a.x * b.y - a.y * b.x;
  }

  friend istream &operator>>(istream &is, Point &p) { return is >> p.x >> p.y; }
};

template <class T>
vector<Point<T>> convex_hull(vector<Point<T>> p) {
  assert(!p.empty());
  sort(p.begin(), p.end(),
       [](const Point<i64> &a, const Point<i64> &b) { return a.x < b.x; });
  vector<Point<T>> u{p[0]}, d{p.back()};
  for (usz i = 1; i < p.size(); ++i) {
    while (u.size() >= 2 &&
           ((u.back() - u[u.size() - 2]) ^ (p[i] - u.back())) > 0)
      u.pop_back();
    u.push_back(p[i]);
  }
  for (usz i = p.size() - 2; (isz)i >= 0; --i) {
    while (d.size() >= 2 &&
           ((d.back() - d[d.size() - 2]) ^ (p[i] - d.back())) > 0)
      d.pop_back();
    d.push_back(p[i]);
  }
  u.insert(u.end(), d.begin() + 1, d.end());
  return u;
}

template <class T>
vector<Point<T>> minkowski_sum(vector<Point<T>> a, vector<Point<T>> b) {
  vector<Point<T>> c{a[0] + b[0]};
  for (usz i = 0; i + 1 < a.size(); ++i) a[i] = a[i + 1] - a[i];
  for (usz i = 0; i + 1 < b.size(); ++i) b[i] = b[i + 1] - b[i];
  a.pop_back(), b.pop_back();
  c.resize(a.size() + b.size() + 1);
  merge(a.begin(), a.end(), b.begin(), b.end(), c.begin() + 1,
        [](const Point<i64> &a, const Point<i64> &b) { return (a ^ b) < 0; });
  for (usz i = 1; i < c.size(); ++i) c[i] = c[i] + c[i - 1];
  return c;
}

int main() {
  cin.tie(nullptr)->sync_with_stdio(false);
  uint32_t n, m, q;
  vector<Point<i64>> a, b;
  cin >> n >> m >> q;
  a.resize(n), b.resize(m);
  for (auto &p : a) cin >> p;
  for (auto &p : b) cin >> p, p = 0 - p;
  a = convex_hull(a), b = convex_hull(b);
  a = minkowski_sum(a, b);
  a.pop_back();
  for (usz i = 1; i < a.size(); ++i) a[i] = a[i] - a[0];
  while (q--) {
    Point<i64> v;
    cin >> v;
    v = v - a[0];
    if (v.x < 0) {
      cout << "0\n";
      continue;
    }
    auto it = upper_bound(
        a.begin() + 1, a.end(), v,
        [](const Point<i64> &a, const Point<i64> &b) { return (a ^ b) < 0; });
    if (it == a.begin() + 1 || it == a.end()) {
      cout << "0\n";
      continue;
    }
    i64 s0 = *it ^ *prev(it), s1 = v ^ *prev(it), s2 = *it ^ v;
    cout << (s1 >= 0 && s2 >= 0 && s1 + s2 <= s0) << '\n';
  }
  return 0;
}

三维凸包

基础知识

圆的反演：反演中心为 \(O\)，反演半径为 \(R\)，若经过 \(O\) 的直线经过 \(P\),\(P'\)，且 \(OP\times OP'=R^{2}\)，则称 \(P\)、\(P'\) 关于 \(O\) 互为反演。

过程

求凸包的过程如下：

  • 首先对其微小扰动，避免出现四点共面的情况。
  • 对于一个已知凸包，新增一个点 \(P\)，将 \(P\) 视作一个点光源，向凸包做射线，可以知道，光线的可见面和不可见面一定是由若干条棱隔开的。
  • 将光的可见面删去，并新增由其分割棱与 \(P\) 构成的平面。 重复此过程即可，由 Pick 定理、欧拉公式（在凸多面体中，其顶点 \(V\)、边数 \(E\) 及面数 \(F\) 满足 \(V−E+F=2\)）和圆的反演，复杂度 \(O(n^2)\)。1

模板题

P4724【模板】三维凸包

重复上述过程即可得到答案。

代码实现 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include <cmath>
#include <cstdlib>
#include <iomanip>
#include <iostream>
using namespace std;
constexpr int N = 2010;
constexpr double eps = 1e-9;
int n, cnt, vis[N][N];
double ans;

double Rand() { return rand() / (double)RAND_MAX; }

double reps() { return (Rand() - 0.5) * eps; }

struct Node {
  double x, y, z;

  void shake() {
    x += reps();
    y += reps();
    z += reps();
  }

  double len() { return sqrt(x * x + y * y + z * z); }

  Node operator-(Node A) const { return {x - A.x, y - A.y, z - A.z}; }

  Node operator*(Node A) const {
    return {y * A.z - z * A.y, z * A.x - x * A.z, x * A.y - y * A.x};
  }

  double operator&(Node A) const { return x * A.x + y * A.y + z * A.z; }
} A[N];

struct Face {
  int v[3];

  Node Normal() { return (A[v[1]] - A[v[0]]) * (A[v[2]] - A[v[0]]); }

  double area() { return Normal().len() / 2.0; }
} f[N], C[N];

int see(Face a, Node b) { return ((b - A[a.v[0]]) & a.Normal()) > 0; }

void Convex_3D() {
  f[++cnt] = {1, 2, 3};
  f[++cnt] = {3, 2, 1};

  for (int i = 4, cc = 0; i <= n; i++) {
    for (int j = 1, v; j <= cnt; j++) {
      if (!(v = see(f[j], A[i]))) C[++cc] = f[j];

      for (int k = 0; k < 3; k++) vis[f[j].v[k]][f[j].v[(k + 1) % 3]] = v;
    }

    for (int j = 1; j <= cnt; j++)
      for (int k = 0; k < 3; k++) {
        int x = f[j].v[k], y = f[j].v[(k + 1) % 3];

        if (vis[x][y] && !vis[y][x]) C[++cc] = {x, y, i};
      }

    for (int j = 1; j <= cc; j++) f[j] = C[j];

    cnt = cc;
    cc = 0;
  }
}

int main() {
  cin >> n;

  for (int i = 1; i <= n; i++) cin >> A[i].x >> A[i].y >> A[i].z, A[i].shake();

  Convex_3D();

  for (int i = 1; i <= cnt; i++) ans += f[i].area();

  cout << fixed << setprecision(3) << ans << '\n';
  return 0;
}

练习

参考资料与注释

  1. 三维凸包学习小记 ↩

本页面最近更新：，更新历史
发现错误？想一起完善？ 在 GitHub 上编辑此页！
本页面贡献者：OI-wiki
本页面的全部内容在 CC BY-SA 4.0 和 SATA 协议之条款下提供，附加条款亦可能应用